Binary on an [] abacus

Here is an image of an abacus: An abacus is a wood frame with sliding beads used for counting and adding. Once you realize what the shortcuts are, they are quite fast, and can be used for adding columns of numbers, balancing your checkbook, and other assorted tasks like doing binary and hexadecimal addition.


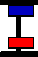
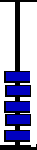
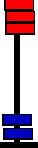
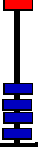
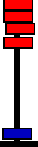
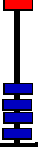
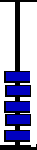
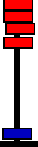
The central bar is used to show a number. The above reads "0314159" or "three hundred and fourteen thousand one hundred and fifty nine." The beads above the center have a decimal value of 5, the beads below the center have a decimal value of 1. The abacus was designed to do base 5 calculations. Using base 5 comes easy to us, maybe because we have five fingers.

.. Binary representation..

To represent binary numbers, just use the upper part of the abacus. Remember two things:

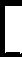
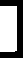
This reads "00011" or "11" if you leave off the leading zeros.

Since the second column (from the right) has a value of 2 the decimal value of 11-bin is ( 1 x 2 ) + 1 = 3-dec. Got that?

.. Binary addition ..

Starting small: add 1-bin to the above number. Result...

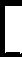
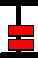
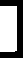
But since "1 + 1" (right column) is equal to "zero, carry one" this should be corrected to...

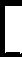
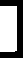
Oops, another correction needed. New result...

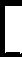
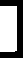
This reads (we were adding 11-bin and 1-bin) as 100-bin. Since the third column has a value of 4, this would be equal to 4-decimal.

Large binary numbers are added the same way. The CPU uses this method for addition as well as multiplication (where repeated addition is used to achieve the result), except that it would use two registers of 16 columns each. The numbers in the two registers are added in a single clock cycle.

.. Hexadecimal representation ..

An abacus can be used to represent hexadecimal numbers too, and can be used to add numbers. Use the following translation of bead values larger than 9..


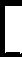
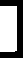
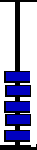
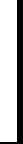10-dec is A in hex


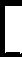
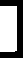
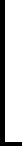
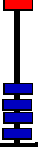
11-dec is B in hex

... and similar for 12, 13, and 14.


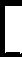
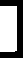
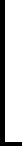
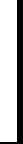15-dec is F in hex

.. and after "F" you carry a "one" to the next column...


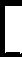
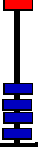
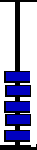
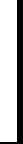This is 10-hex (16-dec).

.. adding hex numbers ..

The example below will add the numbers 3F-hex and 9A-hex, by moving beads from the left to the right.

First enter 3F by sliding beads to the center bar.

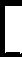
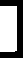3F

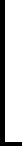
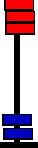
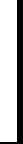
The rightmost column first.. The first step is to add A-hex to the right column. Remember A-hex is 10-dec. So we need to add ten beads to the right column.

But, there is no room for that many additional beads on the right column. But we could add 16 (one bottom bead) to the left column, and subtract 6 from the right column. Results shown below ..

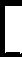
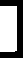49

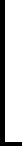
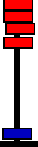
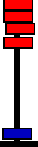
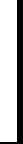
Now to the left column, to add 9: This also is done by adding ten to the left-top column, and subtracting 1 from the left-bottom column. Results shown below ..

D9

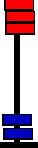
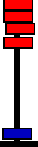
Answer, above, D9. This process can be extended to any number of columns.

[] HOST: Outflux.net, http://www.Outflux.net
URL: http://jnocook.net/user/abacus.htm
19